Let’s begin with the introduction of Group.
What is a group?
A group is a set of elements (collection of things or objects) with an operation that satisfies four specific rules. For example, let’s say you have a set of toy blocks. If you stack one block over another, you get another block.
Note: If the rule of game always work consistently then you have formed a group.
Formally:
A group is a set G with an operation such that the operation is closure, associative, has an identity element, and every element of the set has an inverse element.
You can read more about group here.
Brief History
Group theory begins with studying the symmetry in equations. Early mathematicians like Galois and Gauss explored how groups could describe solutions to polynomial equations and rotations of geometric shapes.
Fun fact: One major breakthrough came from trying to solve the polynomial equation x^5 - x + 1 = 0, where no formula (like quadratic formula) works.
Galois shows that understanding the symmetry of the solutions forms a group and this group tells whether solving the equation is even possible. For more intuition, refer to this.
Importance and Applications of Groups
Groups are everywhere! They are foundational in various fields:
Math: Addition and multiplication are groups; they help solve equations.
Physics: Symmetry groups describe how molecules move or rotate. Read more about this.
Cryptography: Group theory underpins encryption methods like RSA. Read more about this.
Games and Puzzles: The Rubik’s Cube’s moves form a group.
And many more…!
Must know before proceeding further..!
These are the basic concept you should be familiar with!
Set and Operation
A set is simply a collection of distinct objects (elements). Eg: Set of integers {…,-1,0,1,…}.
An operation is something that combines two elements in the set and gives another element in the set.
Eg: Addition(+) on integers.

Fig: Set (source: Wikipedia)
Group Axioms
If any two of its elements are combined through an operation to produce a third element belonging to the same set and meets the four rules i.e. closure, associativity, inverse and identity, they are called group axioms. Read more about it.
Closure:
Combining two elements of a set still results in another element in same set.
Eg: 2 + 3 = 5 (still an integer)
Associativity:
The way you group elements doesn’t affect the result.
Eg: (2 + 3)+ 4 = 2 + (3 + 4) = 9 (Try it with subtraction 😉)
Identity Element:
An element in the set which does nothing when combined with another element of the set.
Eg: 0 + 1 = 1
Idea: Think it as pressing a pause button on a video. The video stays as it is, do nothing!
Inverse:
For every element in a set, there is an opposing element that undoes its effect.
Eg: 2 + (-2) = 0 (Try it in set of integers and multiplication as operation 😉)
Idea: While tying shoelace, every knot has an inverse to untie it.
Examples of Groups
Symmetry Groups:
Set: All transformations (rotations and reflections) of a square.
Operation: Perform one transformation and then another (rotate 90° and reflect).
It satisfies all axioms.
Idea: Imagine flipping or rotating a photo frame. After each move, the frame still looks the same. (maybe the orientation different of course!)
Fig: Symmetry Groups (source: wikipedia)
Integer Addition:
Set: Z = {…,-2,-1,0,1,2,…}.
Operation: Addition(+)
It satisfies all axioms.
Idea: Think of adding an reducing integer weights on a weighing machine.
Matrix Groups:
Set: All n×n matrices.
Operation: Matrix multiplication
It has identity matrix (diagonal of 1s) and inverse matrix too.
Idea: You can relate it to transforming shapes on a graph paper (apply series of transformations to it.)
Subgroups and Cosets
Oh wow, what are these now..?
Subgroup: A subgroup is a smaller group inside a bigger group that still satisfies all group axioms.
Formally, For H to be a subgroup of a group G,
Closure: Combing any two elements of H (using G’s operation) result in an element of H.
Identity: The identity element of G must be an identity element of H.
Inverse: Every element of H must have it’s inverse in H.
Facing little clouds visualizing this..? Let’s proceed with an example.
G = Z (integers under addition)
H = {…,-6,-3,0,3,6,…} multiples of 3.
Closure: Adding two multiples of 3 gives another multiple of 3.
Associativity: (a+b) + c = a + (b + c) where a,b,c ∈ H.
Identity: 0 (also multiple of 3).
Inverse: For every 3, there is -3. Generalization: For every 3a in H, there is -3a in H, where a ∈ G.
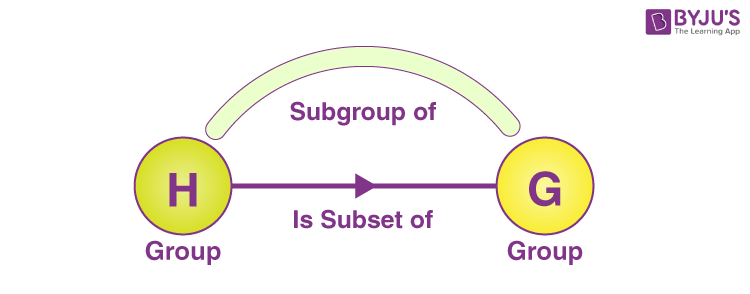
Fig: Subgroups (source: Byju’s)
Cosets: Think it as like the "copies" of the subgroup spread out across the group.
Formally, A coset is formed when you take a subgroup and “shift“ it by multiplying each element by a fixed element from the group.
If G is a group, H is a subgroup, and g ∈ G:
The left coset of H is gH = { g. h | h ∈ H}
The right coset of H is Hg = { h. g | h ∈ H}
Oh wow….! I am little bamboozled. Fine, let’s hop into an example.
Example:
G = Z (integer under addition)
H = {...,−3,0,3,6,...}, multiples of 3.
A left coset of H: 1+H\={...,−2,1,4,7,...}(shifted by 1).
Note: Furthermore, H itself is both a left coset and a right coset. The number of left cosets of H in G is equal to the number of right cosets of H in G. This common value is called the index of H in G and is usually denoted by [G : H]. You can read more about cosets here.
Fig: Cosets (source: wikipedia)
Lagrange’s Theorem
Here it goes..!
Statement: If G is a finite group and H is a subgroup, the size of H (its order) divides the size of G (its order):
|G| = |H| . [G: H]
where [G: H] is the number of cosets of subgroup H in group G (called index).
Significance of Lagrange’s Theorem:
Helps classify groups and their structure.
Tells us how the group is partitioned into equal-sized chunks (cosets).
How can we leave this section without an example…? Let’s dive in:
Eg: G = Z₆ = {0,1,2,3,4,5} (integers mod 6 under addition).
H = {0,3}, multiples of 3.
Order of G is 6. Order of H is 2.
[G : H] = 6 / 2 is 3. It means there are 3 cosets. H, 1+H, 2+H.
Quick Revision for this section:
Subgroup → smaller group that still follows all group axioms.
Coset → shifted version of a subgroup within the group.
Lagrange’s Theorem → links group, subgroups and cosets, helps us understand how group is structured.
Group Properties and Classifications
Finite and Infinite Groups
1. Finite Group
A group is finite if it has limited number of elements. Eg: G = Z₄ = {0,1,2,3} (integers modulo 4 under addition). Operation (+). The group has 4 elements.
2. Infinite Group
A group is infinite if it has unlimited number of elements. Eg: G = Z = {…,-3,-2,-1,0,1,2,3,…} (integers under addition). Operation (+). The group has infinite elements as addition keep producing more elements.
Abelian Groups
A group is Abelian (or commutative) if operation works the same way regardless of the order:
a.b = b.a ∀ a,b ∈ G
Maybe little hard to visualize without an example..?
Abelian group: Integers under addition (Z,+) → 2 + 3 = 3 + 2 = 5.
Non-Abelian group: Rotation of triangle by 120° and flipping isn’t same as flipping first and then rotating.
Let’s get going with some day to day life examples so that this Abelian concept gets set in your mind.
Abelian group: Mixing the sugar in your cup of morning coffee. No matter in what order you stir it, the result would be same.
Non-Abelian group: Getting ready for your college and having to tie your shoe laces. The order of tying the knot matters.
Hope this helps better…!

Fig: Abelian Groups (source: GeeksforGeeks)
Cyclic Groups
A group is cyclic if all its elements can be generated by repeatedly applying the group operation to a single element called generator.
A generator g satisfies: G = {g⁰, g¹, g², …., gⁿ⁻¹}
Finite Cyclic Group: Z₄ = {0,1,2,3} , Generator → 1, operation → + because 0+1 = 1, 1+1 = 2, 2+1 = 3, 3+1 = 0
You can wall clock as an example. Generator → 1, Start at 12, 12 + 1 = 1, 1 + 1 = 2, … after 12 steps it’s back to 12.
Infinite Cyclic Group: Z: Integers under addition, Generator → 1 or -1.
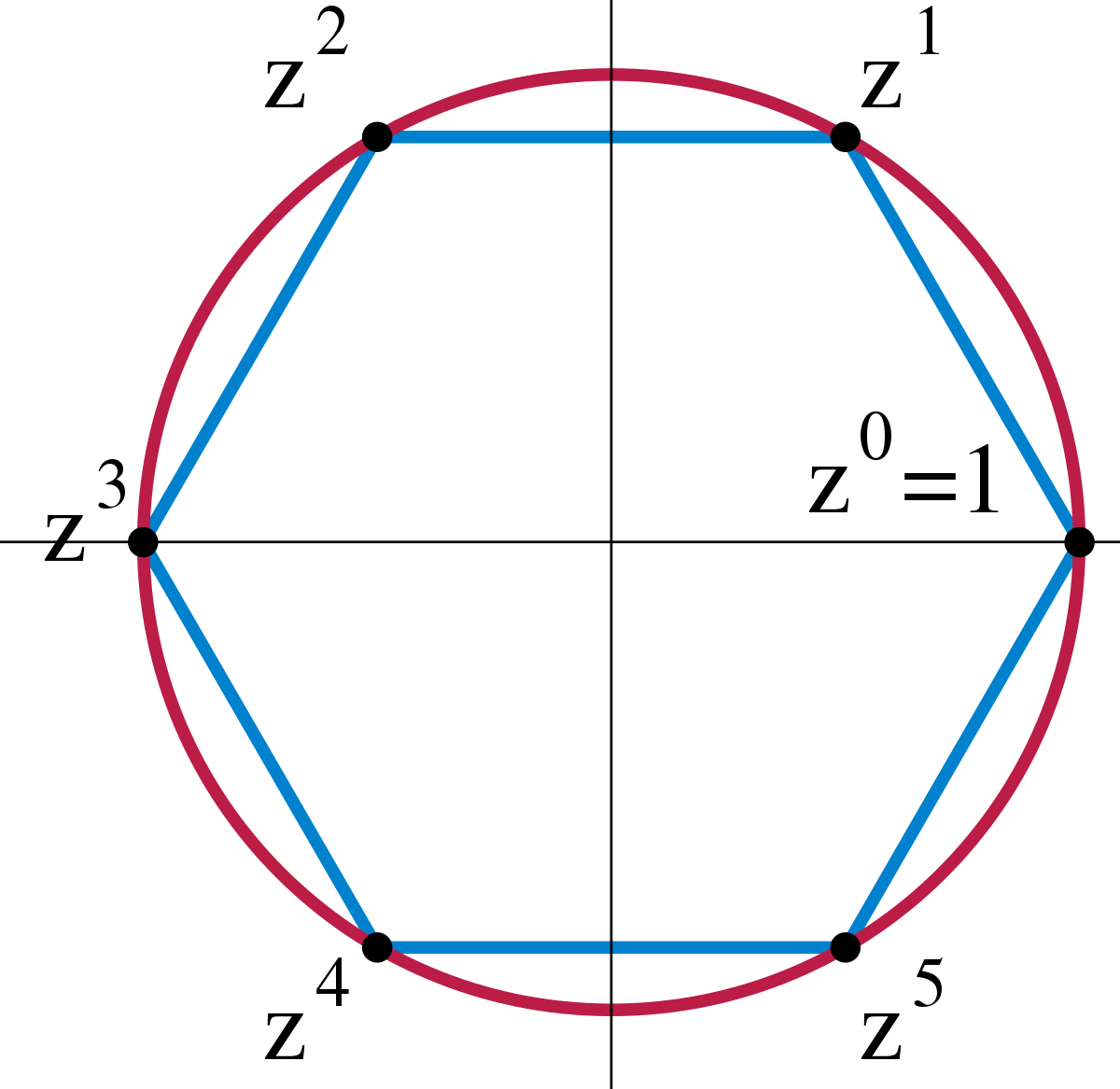
Fig: Cyclic Groups (source: wikipedia)
Order of a Group or Elements
Order of a group → number of elements a group has. Eg: |Z| =∞ (infinite), |Z₄| = 4.
Order of an element → smallest number of times you need to apply group operation to return to identity. Eg: |Z₄| = {0,1,2,3}, the order of 1 = 4 because 1+1+1+1 = 0. (in case of finite group). (Try to find out order of 2 😉).
Hint: 0 + 0 = 0, the order of 0 is 1.
Eg: |Z|, order of every element = ∞ (infinite), because we can never return to 0. (in case of infinite group).
Let’s not make it confusing and solidify the concept for you.
Order of a group → It is like the number of seats in classroom.
Order of an element → It is like counting the number of steps you need to walk around in circle reach the identity (may be the trade mill in your path).
Group Homomorphisms and Isomorphisms
Group Homomorphism
A group homomorphism is a function between two groups that preserves the group operation. If (G,*) and (H, .) are two groups then, a group homomorphism is a function h: G→H such that for all u and v in G, it holds that,
h(u*v) = h(u).h(v) , ∀ u,v ∈ G
where * and . are operations of G and H respectively.
Oh wow, right over the head…!
Eg: Let G = Z (integer under addition) and H = Z₄ (integer mod 4 under addition). Let’s define h: Z → Z₄ by h(x) = x mod 4.
For a = 5, b=3:
h(5+3) = h(8) = 0 (mod 4)
h(5) + h(3) = 1 + 3 = 0 (mod 4)
Thus, h(a+b) = h(a) + h(b), it satisfies homomorphism property.
Fig: Group Homomorphism (source: wikipedia)
May be you got it, if not yet then here is an idea to understand it fully:
Think of Ram, an English to Nepali translator, who translates sentences written in English to Nepali and make them retain meaning as of original. In a group homomorphism, the “meaning“ or “structure“ of operations is preserved between groups.
Kernel of a Homomorphism:
The kernel of h: G → H is the set of elements in G that map to identity in H.
Ker(h) = {g ∈ G | h(g) = eʜ} (where eʜ is identity in H).
Eg: Let h: Z → Z₄ be a map defined by h(x) = x mod 4.
The kernel is {x ∈ Z | x ≡ 0 (mod 4)} = {…,−8,−4,0,4,8,…}
What is it’s significance?
The kernel measures how much information is lost under h.

Fig: Kernel of a homomorphism (source: ResearchGate)
Image of a Homomorphism:
The image of a homomorphism h: G → H is the set of all outputs in H:
Im(h) = {h(g) | g ∈ G}
Eg: For h: Z → Z₄ be a map defined by h(x) = x mod 4,
The image is {0,1,2,3} which are elements of Z₄.
What is it’s significance?
The image shows how much information remains.

Fig: Image of a homomorphism (source: ResearchGate)
Group Isomorphism
A group isomorphism is a special homomorphism that is both one-to-one and onto. Two groups are isomorphic if they are structurally same.
Eg: G = Z₄ = {0,1,2,3} , H = {1,i,-1,-i}
The function h: Z₄ → H defined by h(0) = 1, h(1) = i, h(2)=-1, h(3)=-i is an isomorphism.
What you should understand?
A homomorphism preserves structure between groups, while an isomorphism shows two groups are structurally identical.
The kernel measures “how much is lost” whereas images shows “what remains“ .
Normal Subgroups and Quotient Groups
Normal Subgroups
A normal subgroup N of a group G is a subgroup, that is compatible with the group’s structure.
Formally, ∀ g ∈ G and n ∈ N:
g . n . g⁻¹ ∈ N
Therefore, N looks same however you rotate it within G.
Quotient Groups
A quotient group G/N is formed by collapsing N (a normal subgroup of G) into a single element, dividing G into distinct “cosets“ of N.
What you should understand?
A normal subgroup aligns neatly within the group’s structure.
Quotient groups simplify groups by “collapsing” normal subgroups into a single entity.
Eg: Let G=Z (integers under addition) and N=3Z (multiples of 3).
Cosets are: 0 + N, 1 + N, 2 + N.
Quotient group is Z/3Z, which has 3 elements: {0,1,2} mod 3.
Group Actions
So what is it? Does it mean what it seems to be?
Yes, a group action is a way for group G with an identity element e to “act” on a set X in a way that respects the group structure.
Formally, A group action is a function:
α : G × X → X*,*
that satisfies the following two axioms:
Identity: α (e, x) = x
Compatibility: α (g, α (h, x)) = α (gh, x)
Okay…..!!

Fig: Group Actions (source: wikipedia)
Let’s head straight into an example:
Rotations of a Polygon: Let G be a group of rotations of a triangle (D₃) , and X be the triangle’s vertices. The group action is rotating the triangle such that vertices are permuted. (Hope you know what permutation is…!!)
Still hard to catch…?
Let’s head into a real-life example:
Imagine group action as a control system where G is remote, and X is the remote-control car. The buttons (elements of G) consistently apply transformation to the car.
Learn more about group actions here.
Orbit-stabilizer theorem
Let’s start with, why we need this?
So, we need this theorem because it helps explain how group acts on sets, and how elements in a group interact with each other.
It helps us to count number of distinct configurations that can result from group action.
It can be used to count number of rotational symmetries of a cube.
Let’s say a group G acts on a set X:
The “orbit” of x ∈ X is the set of elements G can move x to:
Orb(x)={g⋅x | g∈G}
The “stabilizer” of x ∈ X is the set of elements in G that leave x unchanged:
Stab(x)={g∈G | g⋅x=x}
Theorem:
For a finite group G, the size of the group relates to the orbit and stabilizer of x:
|G| = |Orb(x)|⋅|Stab(x)|
Eg: Let G = S₃, the group of permutations of X = {a, b, c}. Pick x = a:
The orbit of a is {a,b,c} (a can be sent to all places)
The stabilizer of a is {e,(bc)}, permutation that leaves a fixed.
|G| = 6, |Orb(a)| = 3, |Stab(a)| = 2:
6 = 3 . 2
Advanced Topics in Group Theory
Sylow Theorems
Why we need it?
They provide a method for using a group’s prime decomposition to make statements about its subgroups.
They are specially useful in the classification of finite simple groups.
Note: It gives detailed information about the number of subgroups of fixed order that a given finite group contains.
Theorem: If G is a finite group of order |G|= pⁿ⋅m, where p is a prime, pⁿ divides |G|, and m is not divisible by p:
Existence: G has at least one subgroup of order pⁿ. This is also called Sylow p-subgroup.
Conjugacy: All Sylow p-subgroups are conjugate (structurally the same under a group transformation).
Counting: The number of Sylow p-subgroups divides |G| and is of form 1 + kp.
Let’s head through an example:
Let |G| = 12 = 2² . 3.
G has atleast one Sylow 2-subgroup (order 4).
G has atleast one Sylow 3-subgroup (order 3).
The number of Sylow 2-subgroups divides 12 and is in the form 1 + 2k, thus, possible values are 1 or 3.
Simple Groups and Their Classification
A simple group is a non-trivial group whose only normal subgroups are the trivial group {e} and the group itself.
So what..? Why is it important?
Simple groups are the building blocks of all finite groups, same as the prime numbers for integers.
Classification of finite simple groups: It states that every finite simple group belongs to one of these families:
1. Cyclic groups of prime order.
2. Alternating groups Aₙ (for n ≥ 5).
3. Lie-type groups.
4. 26 sporadic groups (like the famous "Monster group").
Let’s dive into our favorite example section:
Eg: A₅ (the group of even permutations of 5 elements) is a simple group of order 60. No smaller subgroup within A₅ satisfies normality except {e} and A₅ itself.
Idea: You can look simple groups as fundamental atoms in periodic table. Complex compounds are formed by combining these atoms in specific ways.
Free Groups and Generators
Overwhelming…! Why we need it now?
It’s because free groups provide a way to study a pure essence of group structure, unbound by additional constraints.
So, what is it?
A free group is a group in which no relations exist between its generators, except those required by group axioms.
If F is a free group generated by {a, b} , elements are all possible words (finite sequences) of a, b, a⁻¹, b⁻¹:
F={e ,a ,b ,a⁻¹ ,b⁻¹, ab, ba⁻¹,…}.
Eg: A free group generated by a and b contains elements like: a²b⁻¹a⁻³b, where each element is a unique word.
Idea: Treat free groups as writing anything using alphabet where there are no grammar rules, means only the letters matter.
Semidirect Products and Extensions
Now what is its significance..?
Semidirect products generalize direct products by allowing one group to “twist” the other during their combination.
Wow, kind of fascinating…!
So, what is it?
Simply, a semidirect product is a groups having two complementary subgroups one of which is normal.
Formally, the semidirect product is a way to combine two groups N and H into a new group G, where N is normal in G, and H acts on N via automorphisms. It is usually denoted with the symbol ‘⋉’.
Learn more about automorphism here.
I’ll give you a little idea about automorphism. Till now, you must have known about isomorphism. It is simply a structure preserving mapping between two structures of same type (in some sense, mapping to itself) that can be reversed using inverse mapping.
So, automorphism is the isomorphism from a mathematical object (it can be a value that can be assigned to a symbol and then included in a formula) to itself. Read more about mathematical object here.
All rubbish..? Fine let’s get it done via example:
Let N = Z₄ and H = Z₂. Define H acting on N by flipping elements:
h . n = -n (mod 4)
The resulting semidirect product Z₄ ⋊ Z₂ is a non-abelian group (new group is created).
Still not getting it…?
Here an idea to fully grasp it: Think of N and H as two teams collaborating to build something. In a direct product, they work independently, while in a semidirect product, one team influences how the other works. Simple as it, right? You can read more about this here.
What you should understand from this section?
Sylow Theorems: They ensure the existence and count of subgroups of prime power orders.
Simple Groups: They are the fundamental “building blocks“ of group theory.
Free Groups: They are the group with no constraints except group axioms.
Semidirect Products: They are the very powerful way to construct new groups by combining two groups in a “twisted“ way.
Applications of Group Theory
You already got the idea about where group theory is used in our daily lives. Let’s dive a little deep and discuss about it.
Symmetry in Physics and Chemistry
Group theory is used to describe symmetries in molecules, crystals, and physical systems. Symmetry operations (like rotations, reflections, and inversions) form groups called symmetry groups.
In chemistry, It helps explain water molecule(H₂O) dipole moment and interactions in hydrogen bonding. In physics, It is used in crystallography to describe repeating pattern in 3D.
Cryptography: RSA and Discrete Logarithms
The groups of integers modulo n is used to encrypt and decrypt message. Security comes from the difficulty to factor large numbers into primes.
In discrete logarithmic problems, it involves finding x in the equation gˣ ≡ y (mod p), where g is the generator of a cyclic group. This is the base for Diffie-Hellman key exchange and Elliptic Curve Cryptography(ECC).
Rubik’s Cube and Puzzles
The Rubik’s cube is governed by a group G whose elements are all valid moves and the group structure helps to analyze and solve the puzzle.
The Rubik’s cube group has over 4 × 10¹⁹ group elements but the mathematical technique helps reduce the problem by understanding how specific sequences of moves affect the cube’s state.
Lie Groups in Differential Geometry
A Lie Group is a group that has both group structure and smooth, continuous properties. Lie groups connect algebra and geometry.
Symmetry of laws of nature are often described by Lie groups.
For eg, SO(3) (rotational symmetry in 3D space) governs angular momentum in quantum mechanics. The group of rotations SO(3) are used in robotics (to model arm movement) and aerospace (to describe orientation of satellites).
Some important visuals
Diagram of Cayley’s table
Why this?
Cayley’s table are like simple multiplication tables for groups which provides tangible way to visualize group operations.
Eg: Cayley’s table for Z₄:
| + mod 4 | 0 | 1 | 2 | 3 |
| 0 | 0 | 1 | 2 | 3 |
| 1 | 1 | 2 | 3 | 0 |
| 2 | 2 | 3 | 0 | 1 |
| 3 | 3 | 0 | 1 | 2 |
Examples of symmetry groups in real-world objects
Polygon Symmetries
A square’s symmetry group, D₄, includes 8 elements, 4 rotations and 4 reflections.
Molecular Symmetry in Chemistry
The water molecule (H₂O) has a molecular symmetry of C₂𝑣 and has four symmetry elements:Identity: E
2nd order axis of symmetry: C₂
Two symmetry planes: 𝜎𝑣
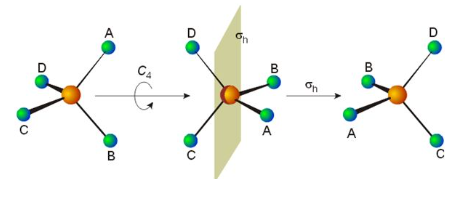
<p align="center">Fig: Symmetry of water in chemistry (source: wikipedia)</p>
Crystal Structure

Fig: A cube with it’s planes of symmetry (Source: ResearchGate)
Exercises and Problems
You can solidify your learning by practicing these problems.
Basic Problems
Check group axioms.
Prove that (Z, +), the set of integers under addition is a group.
(Hint: sum always integer? a + e = a? a + b = e?)Is (N, +), set of natural number under addition a group? Why or why not?
(Hint: Does N include negatives to satisfy inverses? )
Cayley’s table Verification.
Construct the Cayley table for Z₄ under addition modulo 4. Verify the closure, identity, and inverse properties using the table.
(Hint: Write group operation as addition modulo 4 and check for identity and inverses as above.)
Symmetry Group Exploration.
List all elements of the symmetry group D₄ for a square and describe their operations (rotations and reflections). Verify the group properties.
(Hint: Turn square 0°, 90°, 180°, and 270°. Flip vertical, horizontal and diagonal. Verify closure combining any two operations.)
Bonus one: Show that the set {1,−1} under multiplication is a group. What type of group is this?
(Hint: Analyze above questions and you can do this too. )
Intermediate Problems
Homomorphism Verification
Define a map, h:Z → Z₄, by h(n) = n mod 4. Prove that h is a group homomorphism.
Find the kernel and image of h.(Hint: Check if h(a + b) = h(a) + h(b) mod 4, for kernel, solve h(n) = 0 mod 4, for image, set of all outputs of h.)
Coset Construction
Let H = {0,4,8} ⊂ Z₁₂. Find all the left cosets of H in Z₁₂.
Prove that the number of cosets equals the index of H in Z₁₂.(Hint: Write all the elements of H. Left coset: for each a, a + H = a+h mod 12, h∈H)
Order of Elements
In the group Z₆, find the order of each element. And, prove that the order of an element in a finite group divides the order of the group.
(Hint: Compute a, 2a, 3a, ….until cycle returns back to identity ‘0‘.)
Bonus one: Prove that the kernel of a homomorphism is a normal subgroup of the domain group.
(Hint: Recall normality and use the homomorphism property.)
Advanced Problems
Prove Sylow’s First Theorem
Let G be a group of order 56. Use Sylow’s theorems to determine the possible numbers of Sylow 7-subgroups in G.(Hint: For |G| = 56 = 2³ . 7)
Classify Groups of Order 4
Classify all groups of order 4 up to isomorphism. Prove that there are exactly two such groups.
(Hint: Consider Z₄ and Z₂×Z₂ and compare these group structure.)Normal Subgroups and Quotient Groups
Let G=S₃, the symmetric group of degree 3. Identify all normal subgroups of G.₃ Construct the corresponding quotient groups and describe their structure.
(Hint: S₃ has 6 elements, list them (identity, 3 transposition and 2 cycles))Group Automorphisms
Determine all automorphisms of Z₆. Prove that the automorphism group of Z₆ is isomorphic to Z₂×Z₂.
(Hint: Find all h: Z₆ → Z₆ that preserves addition modulo 6 and compare the group structure.)
(Bonus Hint: Z₆ is cyclic, generated by 1 and automorphism maps generator to generator.)
Bonus one: Prove that any group of order p² (where p is a prime) is abelian. Classify all such groups.
(Hint: Use Lagrange’s theorem to deduce the order of every element to p². Consider the center Z(G) and show it’s non-trivial.)
Conclusion
Group theory is an important concept in mathematics which offers tools to analyze symmetry, transformations and algebraic structures. It connects diverse fields, from physics to chemistry to cryptography and computer science. Studying group theory will help you to unlock the ability to study and classify groups and their behavior.
Important Links
Youtube Playlist: https://www.youtube.com/playlist?list=PLDcSwjT2BF_VuNbn8HiHZKKy59SgnIAeO
Wikipedia: https://en.wikipedia.org/wiki/Group_theory
Discussions: https://math.stackexchange.com/search?tab=votes&q=user%3a12952%20%5bgroup-theory%5d

